The Reference Frame: The holographic principle

The newest episode of The Big Bang Theory that was aired last night was called "The Holographic Excitation" (S06E05).

It's pretty cool that a TV sitcom manages not only to show a hologram but Leonard Hofstadter was even allowed to present a rather accurate definition of the holographic principle in quantum gravity i.e. string theory (you won't find it in any popular science TV program that claims to explain modern physics!). And as a result, he was able to have an intercourse with Penny right after she wore some glasses and was shown a moving holographic pencil and a moving holographic globe. (Later, he repeated the same achievement using Maglev.)

(And I even think that Prof Nina Byers whom I know rather well walks behind the main actors around 9:15. This theory seems to make sense because she's at UCLA, much like the TBBT science adviser David Saltzberg.)

The holographic principle of quantum gravity is an incredible example of the ability of the quantum gravity and string theory research to teach us things we really didn't and perhaps couldn't anticipate, force us to modify or abandon some prejudices, and adopt ideas about the unification of ideas and concepts that philosophers couldn't have invented after thousands of years of disciplined reasoning but physicists may be forced to realize them if they carefully follow the mathematical arguments sprinkling from a theory that they randomly discovered in a cave.

But let's return half a century into the past. Holography started in "everyday life physics" in the late 1940s.

So let us begin with this exercise in wave optics that has nothing to do with quantum gravity or string theory so far ? but you will see that it exhibits a similar mechanism that is apparently "recycled" by the laws of quantum gravity.

Dennis Gabor's 3D images

Hungarian-British physicist Dennis Gabor was playing with X-ray microscopy and invented a new technology that is rather cute. One may create two-dimensional patterns on a piece of film which, when illuminated by a laser, create the illusion of a three-dimensional object floating in the space around it. I saw my first hologram sometime in 1985 ? it was a Soviet one, the mascot of the 1980 Olympics in Moscow ? in the National Technological Museum in Prague where we went to a school excursion. I couldn't believe my eyes. :-)

The basic setup involves a monochromatic laser beam, some interference, and a photographic plate. First, we must create the hologram ? a film with strip-like patterns that don't resemble the bear at all but which allow the bear to jump out once you use another laser. Fine. Let's create a hologram.

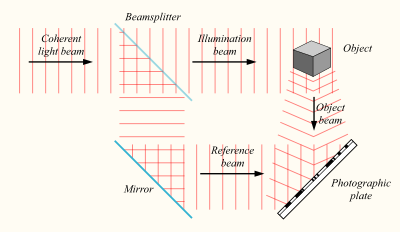
You see that a monochromatic (one sharp frequency) laser beam is coming from the upper left corner. Each photon's wave function gets divided into two portions by a beam splitter ? note that the wave function has a probabilistic interpretation for one particle but if many photons are in the same state, it may be interpreted as a classical field.

Two parts of the wave are moving from the beamsplitter. One gets reflected from a simple mirror. More interestingly, the other one gets reflected from the object we want to see on the hologram. They interfere ? these waves are recombined ? in the right lower corner and they create a system of interference strips on the photographic plate.

We have created a hologram and now we may sell it. What will the buyers do with it?

This interference pattern may be shined upon by a "reconstruction beam" of the same frequency and what we see is a virtual image behind the plate. You may actually move your head and eyes and the position of all points on the image are moving just like if the virtual image were a real object. So it's not just a stereographic image offering two different pictures for the two eyes: the hologram is ready to provide the right electromagnetic field regardless of the direction from which you observe it! If you want to see the right face of the object, you move your head to the right side, and so on.

Why does it work? It's very useful to think about the hologram for a simple object, e.g. a point at a given distance. The total wave function on the photographic plate parameterized by coordinates \(x,y\) is given by \(U_O + U_R\) where \(U_O\) is the complicated wave reflected from the object and \(U_R\) is the simple reference beam reflected from the plain mirror.

You may imagine that for an object being a point, \(U_R=1\) and \(U_O(x,y)=\exp(iks(x,y))\) where \(s\) is the distance between the point (the real object we want to holographically photograph) and the given point \((x,y)\) on the photographic plate. The wave number is of course the inverse wavelength, \(k=2\pi/\lambda\). The sum \(U_R+U_O\) gives you some simple concentric circles (with decreasing distances between neighbors) around the point on the plate that is closest to the photographed point. Fine. The total intensity ? how much the point on the film changes the color ? is given by \[

T \sim \abs{U_O}^2 + \abs{U_R}^2 + U_R^* U_O + U_O^* U_R.

\] I omitted an unimportant overall normalization and used the symbol \(T\) for this quantity because the darkness of the point of the film will be interpreted as the transmittance, the ability of the place of the hologram to transmit the other, reconstruction beam when we actually want to reconstruct the image.

For a simple explanation why you will see the reconstructed virtual image, assume that the reference beam \(U_R\) is much stronger than the object-induced wave \(U_O\) i.e. \(U_R\gg U_O\). So the total wave function may be written as \[

U = 1 + \varepsilon \exp(iks)

\] where \(\varepsilon\) is small, \(\varepsilon\ll 1\). You see that the squared absolute value is\[

T \sim |U|^2 = 1 + \varepsilon \exp(iks) + \varepsilon \exp(-iks) + {\mathcal O}(\varepsilon^2).

\] Imagine that this transmittance is just multiplying another simple reference beam \(U_R\to T \cdot U_R\) and produces some electromagnetic field in the vicinity of the hologram. For the sake of simplicity, assume \(U_R=1\) again. It's only \(U_O\) that carries the "complicated information about the photographed object" but we still need some nonzero \(U_R\).

You may see that \(T\) is almost the same thing as \(U\) except that it has an extra, complex conjugate term. So the electromagnetic field in front of the hologram (on the side with the air) will be the same field as the electromagnetic field we used to have when there was a real object in front of the hologram plus some complex conjugate term. One of these terms creates a nice virtual image behind the plate because it has a similar mathematical structure and when the fields have the same values, we see the same thing.

The other term induces the feeling of another copy of the object ? a real image. It's because all the waves should also be multiplied by the universal time-dependent factor \(\exp(-i\omega t)\) (before you interpret the real and imaginary value of the overall sum as the electric and magnetic fields, respectively, kind of) and the complex conjugation is equivalent to \(t\to -t\) which means that the wave is kind of moving backwards in time which is effectively equivalent to moving from the other side of the mirror.

So when you look at the hologram, you actually see one virtual image behind the plate and one real image in front of the plate (which may overlap with your head). I don't want to figure out which term is which because odds would be close to 50% that my answer would be wrong. To be sure about the answer to this not-so-critical question, I would have to decompose the electromagnetic wave to the electric and magnetic components, consider \(x\) and \(y\) polarizations, be careful about the spatial dependence and all the signs, etc. But things clearly work up to this "which is which" question that I am not too interested in.

In this brute calculation, I have neglected the \({\mathcal O}(\varepsilon^2)\) terms which indicates that the hologram will be badly perturbed if \(\varepsilon\sim {\mathcal O}(1)\) but a more accurate analysis shows that the result won't be too bad even if you include these second-order terms. At any rate, I have created a virtual image of a point! By the superposition principle, you are allowed to envision any object to be composed of many points (perhaps as an "integral of them") and add the terms \(\exp(iks_P)\) from each point \(P\) and you get the idea how it work for a general object.

There exist generalizations ? colorful holograms, perhaps moving holograms and holographic TV, and so on, but I don't want to go into these topics on the boundary of physics and engineering. Everyone knows that holograms are cool. What's important for us is that they store much more than some two-dimensional projections of a 3D object as seen from one direction or two directions; they store the information about the 3D object as seen from any direction (in an interval). They're the whole thing.

Instead of discussing advanced topics of holography in wave optics, we want to switch to the real topic, the holographic principle in quantum gravity.

The holographic principle

In the research of quantum gravity, the notion of holography was introduced by somewhat speculative but highly playful papers by Gerard 't Hooft in 1993 and Lenny Susskind in 1994. Charles Thorn is mentioned as having suspected similar ideas for years.

It may sound unusual ;-) but Lenny Susskind's paper was the technically more detailed one, getting well beyond the hot philosophical buzzwords. Susskind also suppressed some unjustified and unjustifiable "digital" comments by 't Hooft who had written that the information had to be encoded in binary digits (bits). Of course, there's no reason whatsoever why it couldn't be trinary digits, other digits, or ? much more likely ? (for humans and computers) some much less readable but more natural codes.

What's the basic logic behind holography in quantum gravity?

In classical general relativity, a black hole is the final stage of the collapse of a star or another massive object. Because the entropy never decreases, as the second law of thermodynamics demands, the "final stage" must also be the stage with the maximum entropy. So the black hole has the highest entropy among all bound or localized objects of the same mass (and the same values of charges and the angular momentum). I emphasize the adjectives "bound or localized" because delocalized arrangements of particles with a given total energy ? e.g. the Hawking radiation resulting from a black hole that has already evaporated ? may carry a higher entropy (that's inevitably the case because the process of Hawking radiation must be increasing the total entropy, too).

But we've known from the insights by Jacob Bekenstein and Stephen Hawking in the 1970s that the black hole entropy is\[

S_{BH} = \frac{A}{4G}

\] in the relativistic \(c=\hbar=1\) units. It's one-quarter of the area of the event horizon \(A\) in the units of the Planck area. In normal units, you must replace\[

G \to l_{\rm Planck}^2 \equiv \frac{G\hbar}{c^3}.

\] So the maximum entropy of a bound localized object of a given mass is actually given by the area of the black hole of the same mass. Because you can't really squeeze the matter into higher densities than the black hole, the black hole is also the "smallest object" that may contain the given mass.

To summarize, we see that the black hole is the "highest entropy" object as well as the "geometrically smallest" object among localized or bound objects of the given mass. It follows that it also maximizes the "entropy density" (entropy per unit volume) among the localized arrangement of matter of the same total mass. But the entropy carried by a black hole is only proportional to the surface area in the Planck units, \({\mathcal O}(R^2)\), so the entropy density per unit volume ? the latter scales as \({\mathcal O}(R^3)\) ? is therefore going to zero for large black holes i.e. for large masses or large regions.

The maximum density of entropy or information you may achieve with a given mass is actually going to zero if the mass is sent to infinity. If you try to squeeze too many memory chips into your warehouse, they will start to be heavy at some point and will gravitationally collapse and create a black hole which will have a certain radius ? either smaller than or larger than your warehouse. At any rate, this black hole will only be able to carry \(1/4\) of a nat (a bit is \(\ln(2)\) nats) of information per unit surface area (by the surface, I mean the event horizon).

We see that the maximum information is carried by a constant density per unit area rather than the unit volume. You should appreciate how shocking it is. In some sense, it was completely unexpected by virtually all experts in the field. Quantum field theories predict some new phenomena at a characteristic distance scale. For example, Quantum Chromodynamics (QCD) says that quarks like to bind themselves into bound states where their distance is comparable to the QCD length scale, about one fermi or \(10^{-15}\) meters. So by the dimensional analysis, the only sensible "density of information" we may get in QCD is "approximately one bit per cubic fermi" or per "volume of the proton".

People would expect a similar thing in any QFT ? which was mostly right ? but they thought it would also hold in quantum gravity. So quantum gravity may achieve "one bit per Planck volume". But that was wrong. You see that the previous paragraph assumed a bit more than the dimensional analysis: it also implicitly and uncritically postulated that the information is proportional to the volume. This assumption followed from locality. But this assumption breaks down in quantum gravity where the information only scales as the surface area.

Because the "proportionality to the volume" is linked to "locality" ? each unit volume is independent from others ? the violation of the "proportionality of the information to the volume" that the holographic principle forces upon us also means that locality is violated, at least to some extent. And indeed, this violation of the locality is a fact responsible for the resolution of other puzzling questions in quantum gravity, too. In particular, some tiny and hard to observe but nevertheless real non-locality occurs during the evaporation of the black hole which is why the information may get from the black hole interior to infinity, after all ? even though classical general relativity strictly prohibits such an acausal export of the information (locally, it's equivalent to the superluminal transport of information which was already banned in special relativity). In quantum gravity, this "ban" is softened because the information may temporarily violate the rule in analogy with the quantum tunneling. In fact, the black hole evaporation is a version of quantum tunneling.

Whether the holographic principle was real and what it exactly it meant and what it didn't mean remained a somewhat open question for 3 more years or so. However, at the end of 1997, Juan Maldacena presented his AdS/CFT correspondence which is a set of totally controllable mathematical frameworks in which holography holds. The information about a region ? namely the whole anti de Sitter space ? is stored at the boundary of the region ? which is the asymptotic region at infinity which nevertheless looks like a "finite surface of a cylindrical Penrose diagram" if you use the language of Penrose causal diagrams.

The holographic principle surely captures the right "spirit" of quantum gravity but it is a bit vague. The AdS/CFT correspondence is a totally well-defined "refinement" of the holographic principle but it is arguably too special. Nevertheless, one must be careful about deriving potentially invalid corollaries of the holographic principle in other contexts.

For example, if you replace the anti de Sitter space by a finite-volume region of ordinary space, it seems clear to me that the holographic principle will only be true in some rather modest sense: it will be true that the entropy bounds hold. You can't squeeze too much entropy into a given region. However, if you will try to find the "theory on the boundary" that is equivalent to the evolution inside the region, you will find out that such a theory on the boundary "exists" ? but the existence of such a theory is just an awkward translation of the ordinary evolution to some artificial degrees of freedom that you placed on the boundary.

What is special about the AdS/CFT correspondence is that the theory on the boundary is a theory of a completely normal type ? namely a perfectly local, conformal quantum field theory. In fact, the boundary theory is more local than the gravitational theory in the bulk ? because we just said that the gravitating theory in the bulk must be somewhat non-local. I am confident this fact depends on the infinite warp factor of the AdS space at infinity and won't hold for finite regions. In other words, I think that the "holographic theory living on a boundary" of a generic finite region won't be local in any sense ? the boundary still has a preferred length scale, the Planck length, and other things so it is surely not conformal etc. And because it won't be local, it won't be simple or useful, either.

So one shouldn't generalize the holographic principle as seen in the AdS/CFT correspondence too far and too naively.

Lessons

In the 1970s, people got used to Ken Wilson's "Renormalization Group" inspired thinking about all effective field theories. Each theory predicted some phenomena at a characteristic length scale. The third power of the length scale gave us a characteristic volume. And one could expect roughly one nat (or bit) per one characteristic volume. It was nice, it made sense, it has lots of applications.

But Nature sometimes has surprises in store and quantum gravity had one, too. You may still use almost the same logic ? one nat per unit region ? but the region must actually be measured by its surface area, not its volume. So quantum gravity tells us that one of the spatial dimensions may be thought of as an "artificial" or "emergent" one and other mechanisms supporting this general paradigm have appeared as well.

A brutally arrogant yet extremely limited physicist who really sucks ? think of Lee Smolin, for example ? may think that he has all the right ideas how the final theory should look like from the beginning. Except that none of them works (except as tools to impress some stupid laymen). But other physicists who are much smarter but much more modest may see that all Smolin's prejudices are just wrong and Nature's inner organization is much more clever, creative, surprising, and forcing us to learn new concepts and new way of thinking more often than Smolin and many others would expect. One must still be ingenious or semi-ingenious to discover some important wisdom about Nature ? e.g. holography and the AdS/CFT correspondence ? but Nature just doesn't appreciate men who try to paint themselves as wiser than herself. Science is the process of convergence towards Her great wisdom; it is not a pissing contest in which idiots such as Lee Smolin try to pretend that they're smarter than Nature.

The story of the holographic principle also shows us that Nature recycles many ideas. The fields defined on the boundary CFT in the AdS/CFT correspondence literally emulate the waves \(U\) and \(T\) that I mentioned in the discussion of the "ordinary" holography by Dennis Gabor.

And the story of the holographic principle is another anecdotal piece of evidence in favor of the assertion that string/M-theory contains all the good ideas in physics. 't Hooft and Susskind, building on the work by Bekenstein, Hawking, and others, had some "feelings" about the right theory of quantum gravity and there had to be something right about them. And indeed, string theory showed us that they were mostly right. Because string theory is a much more mathematically well-defined a structure than "quantum gravity without adjectives", it also allowed us to convert the philosophical speculations into sharp and rigorous mathematical structures and equations and decide which of the philosophical speculations may be proven as meaningful ones and which can't.

The holographic principle is also another step in the evolution of physics that makes our theories "increasingly more quantum mechanical". While the spacetime remains continuous, we see that the information in a region may be bounded in unexpected ways and a whole dimension of space may be emergent. Needless to say, the equivalence between theories that disagree about the number of spacetime dimensions is only possible if you take the effects of quantum mechanics into account.

Source: http://motls.blogspot.com/2012/10/the-holographic-principle.html

heidi klum and seal ohare airport etta james songs east west shrine game haywire underworld awakening dog the bounty hunter